Overview

Build and Release Status

Pipeline	Status
Master Build
Latest Release

Introduction

The SentryOne Unit Test Generator extension generates tests for classes written in C#. The extension covers basic tests automatically (for example, checking for correct property initialization), and creates placeholder tests for methods.

Test Project organization is simple and automatic because the tests are created in the test project with the same hierarchy defined in the source project. The extension can be used to modify tests later in the life cycle after refactoring or adding new functionality:

• Add tests for new methods
• Regenerate tests as needed

Supported Frameworks

The following test frameworks are supported:

• MSTest
• NUnit
• xUnit

The following mocking frameworks are supported:

• NSubstitute
• Moq
• Rhino Mocks
• FakeItEasy

Using the Extension

After installation, open the extension through:

• The solution explorer context menu
• The code editor context menu

Extension Functions

The following functions are available:

• Generate tests - generates tests for the selected entity.
• Go to tests - opens the file containing the tests for the selected object. This option also works if you are selecting a member in the code window.
• Regenerate tests - replaces existing tests with new ones. This is useful for cases like changes in a constructor signature.

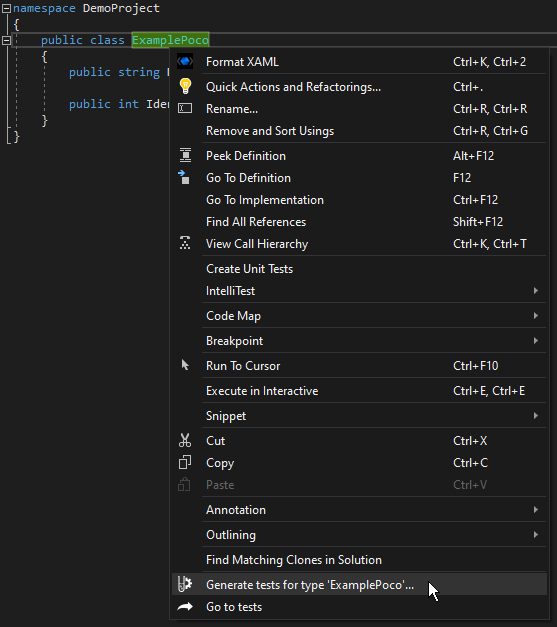
Important: Regenerating a test will replace any code that you have added to the test class or method that is being regenerated. Please use this with care.

Using the code editor context menu:

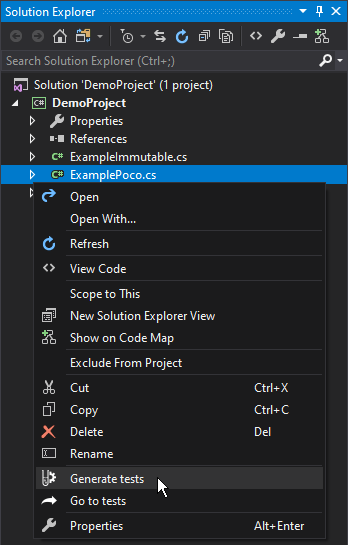
Using the solution explorer context menu:

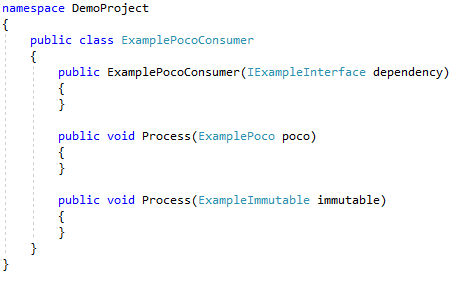
Regenerate tests and Go to tests are not available at higher levels in the solution explorer (for example when you have a folder or project selected). Regenerate tests is not shown by default, to prevent accidental overwriting of test code. Hold SHIFT while you open the context menu to use this option.

Use Case

Consider this simple class:

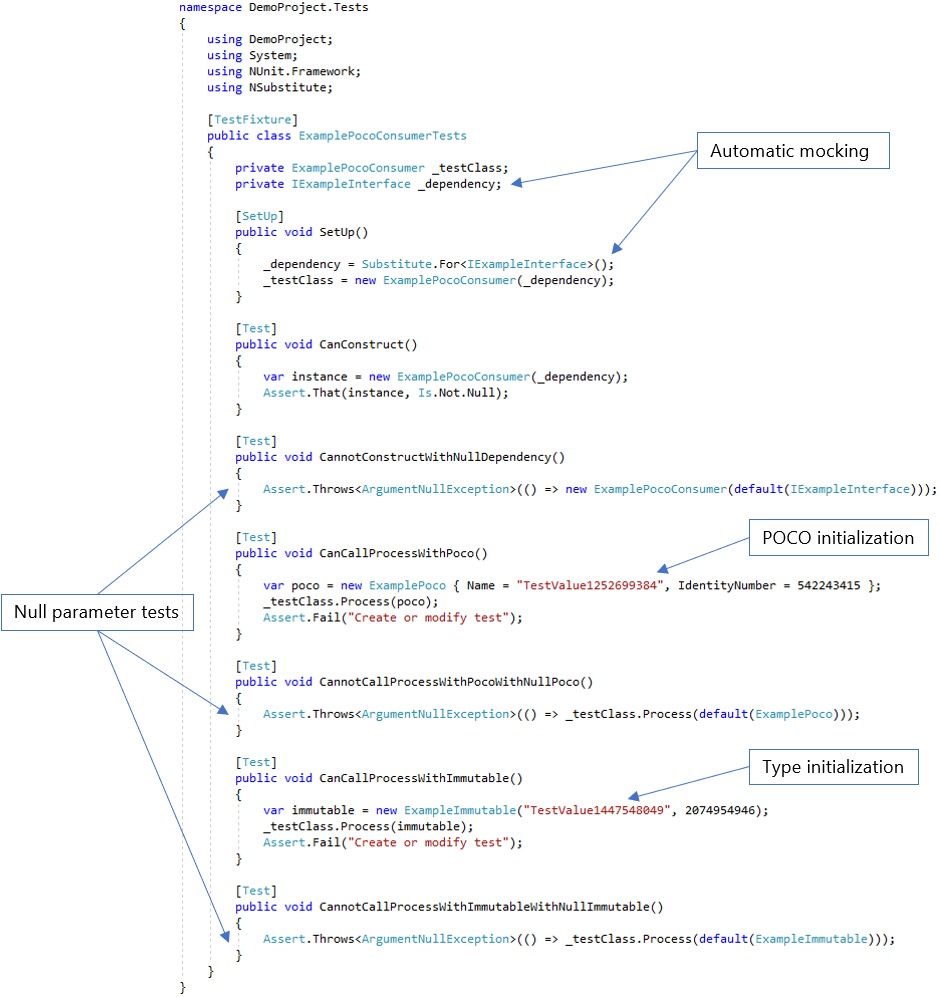
Although the constructor and methods are not implemented, it serves as a good example because the extension generates tests based on signatures only. The following illustrates the results of generating tests for this class.

Notice that the dependency for the class has been automatically mocked & injected, and there are generated tests for the constructor. There are also tests to verify that parameters can’t be null for both constructors and methods. Note that the generator is producing values required for testing – both initializing a POCO using an object initializer and an immutable class by providing values for its constructor.

Controlling the process

The Unit Test Generator extension options page allows for control of various aspects of the process. Generation Side

• Select the test and mocking frameworks to be used
• Control the naming conventions for: test projects, classes, and files

Note: The default for project naming is ‘{0}.Tests’. For example, a project named MyProject would be associated with a test project called MyProject.Tests.

Note: The default for the class and file naming is ‘{0}Tests’. For example, a class called MyClass would be associated with a test class called MyClassTests.

Other Options

• Control whether test projects are automatically created
• Control whether references are automatically added to test projects
• Control the version of the framework dependencies that’s used

Note: If these options are not set, the extension uses the latest version. This does not apply to NUnit 2 because NUnit 2 and NUnit 3 share the same NuGet package name and the NUnit 2 version will always be 2.6.4 if this is left blank.

Setting options per-solution

You can set settings per-solution if you need to (for example if you work with some code that uses MSTest and some that uses NUnit). In order to do this, you can create a .unitTestGeneratorConfig file, which is formatted similarly to .editorConfig files, just without the file type heading.

You can set any member of the IGenerationOptions or the IVersioningOptions interfaces using this method. For example, the following content in a .unitTestGeneratorConfig would set the test framework to MSTest, the mocking framework to NSubstitute and the test project naming convention to <project_name>.UnitTests:

test_project_naming={0}.UnitTests
framework-type=MSTest
MockingFrameworkType=NSubstitute

Note that the formatting for the member names is case insensitive, and underscores and hyphens are ignored. Hence frameworkType, framework-type, FRAMEWORK_TYPE and FRAME-WORK-TYPE all resolve to the FrameworkType member of IGenerationOptions. The rules for file finding & resolution work exactly the same as they do for .editorConfig files - in short, all folders from the solution file to the root are searched for a .unitTestGeneratorConfig file, and files 'closer' to the solution file take precedence if the same option is set in more than one file.

Other Notes

Important: Currently the extension doesn’t handle automatically creating test projects for .NET Core apps. It works as expected with.NET framework and .NET Standard projects. For .NET Core apps, please create the test project manually. Adding test classes and methods works normally once the project is in place.